Logische raadsels
13 raadsels
Welke letter ontbreekt in deze reeks?
Antwoord: S (SATURNUS, eerste letter van de planeten)
Het getal 21 komt ook voor in de rij van Conway. Welk getal vult deze rij aan?
Antwoord: 312211
In Gent wonen een aantal studenten samen in een studentenhuis waar enkel Grieks, Italiaans en Engels gesproken wordt. 3 studenten spreken Grieks, Italiaans en Engels. 7 studenten spreken Engels. Twee studenten zijn tweetalig en spreken enkel Grieks en Italiaans. Één studentje spreekt Engels en Grieks. Eén van de studenten spreekt alleen maar Italiaans en drie alleen maar Grieks. Hoeveel studenten wonen er in het studentenhuis?
Antwoord: 13
Thomas en zijn vrouw hielden thuis een feestje met 4 andere getrouwde stellen. Elk persoon heeft handen geschud met iedereen die hij of zij nog niet kende. Nadat het handen schudden voorbij was, vroeg Thomas iedereen, inclusief zijn vrouw, hoeveel handen zij geschud hadden. Tot zijn verbazing kreeg Thomas negen verschillende antwoorden.
Hoeveel handen heeft de vrouw van Thomas geschud?
Antwoord: Omdat niemand natuurlijk handen geschud heeft met zichzelf of met zijn of haar partner, heeft niemand met meer dan acht personen handen geschud. En omdat negen personen handen geschud hebben met verschillende aantallen mensen, moeten deze aantallen 0, 1, 2, 3, 4, 5, 6, 7 en 8 zijn.
De persoon die 8 handen heeft geschud, heeft handen geschud met alle andere personen (die dus elk ten minste 1 keer handen hebben geschud), behalve met zijn of haar partner. De partner van de persoon die 8 handen heeft geschud, moet dus de persoon zijn die 0 handen heeft geschud.
De persoon die 7 handen heeft geschud, heeft handen geschud met alle andere personen (die dus elk ten minste 2 keer handen hebben geschud), behalve met zijn of haar partner en de persoon die 0 handen heeft geschud. De partner van de persoon die 7 handen heeft geschud, moet dus de persoon zijn die 1 hand heeft geschud.
De persoon die 6 handen heeft geschud, heeft handen geschud met alle andere personen (die dus elk ten minste 3 keer handen hebben geschud), behalve met zijn of haar partner en de personen die 1 en 0 handen hebben geschud. De partner van de persoon die 6 handen heeft geschud, moet dus de persoon zijn die 2 handen heeft geschud.
De persoon die 5 handen heeft geschud, heeft handen geschud met alle andere personen (die dus elk ten minste 4 keer handen hebben geschud), behalve met zijn of haar partner en de personen die 2, 1 en 0 handen hebben geschud. De partner van de persoon die 5 handen heeft geschud, moet dus de persoon zijn die 3 handen heeft geschud.
De enige overgebleven persoon is degene die 4 handen geschud heeft, en is dus Thomas vrouw. Het antwoord is daarom: Thomas vrouw heeft 4 handen geschud.
Flurkske is een vreemde leugenaar. Zes dagen van de week liegt hij, maar op die ene andere vaste dag spreekt hij altijd de waarheid. De volgende uitspraken deed hij op drie opeenvolgende dagen:
- Dag 1: "Ik lieg op maandag en dinsdag."
- Dag 2: "Vandaag is het donderdag, zaterdag of zondag."
- Dag 3: "Ik lieg op woensdag en vrijdag."
Op welke dag van de week spreekt Flurkske de waarheid?
Antwoord: Flurkske spreekt slechts op 1 dag de waarheid. Wanneer de uitspraak op dag 1 onwaar is, betekent dit dus dat hij de waarheid spreekt op maandag of dinsdag. Wanneer de uitspraak op dag 3 onwaar is, betekent dit dat hij de waarheid spreekt op woensdag of vrijdag. Omdat Flurkske op slechts 1 dag de waarheid spreekt, kunnen deze uitspraken niet beide onwaar zijn. Precies één van deze uitspraken moet dus waar zijn, en de uitspraak op dag 2 moet onwaar zijn.
Stel dat de uitspraak op dag 1 waar is. De uitspraak op dag 3 is dan onwaar, waaruit volgt dat Flurkske de waarheid spreekt op woensdag of vrijdag. Dus dag 1 is een woensdag of een vrijdag. Dag 2 is dan dus een donderdag of een zaterdag. Dit zou echter betekenen dat de uitspraak op dag 2 waar is, wat niet kan. Hieruit volgt dat de uitspraak op dag 1 onwaar is.
Dit betekent dat Flurkske de waarheid sprak op dag 3 en dat dit een maandag of dinsdag is. Dag 2 is dus een zondag of een maandag. Omdat de uitspraak op dag 2 onwaar moet zijn, volgt dat dag 2 een maandag is.
Dag 3 is dus een dinsdag. De dag waarop Flurkske de waarheid spreekt is dus dinsdag.
Er liggen vier kaarten op tafel, waarover iemand het volgende beweert: "Als er op de ene kant van de kaart een klinker staat, dan staat op de andere kant van de kaart een even getal."
Welk(e) kaart(en) moet je noodzakelijk omdraaien om te weten of die stelling klopt?
Antwoord: De A en de 7 moet je omdraaien.
De A moet omgedraaid worden om te kijken er een even cijfer op de andere zijde staat. Als er een oneven cijfer op de andere zijde staat, is de bewering fout.
De 7 moet omgedraaid worden om te controleren dat er géén klinker op de andere zijde staat. Als er een klinker op de andere zijde staat, is de bewering fout.
De D moet niet omgedraaid te worden, het is immers geen klinker en het maakt dus niet uit wat voor cijfer er op de andere zijde staat.
De 4 moet ook niet omgedraaid te worden. Of er nu een klinker of een medeklinker op de andere zijde staat, de kaart voldoet altijd aan de bewering: er wordt immers niet beweerd dat alleen kaarten met een klinker een even cijfer op de andere zijde hebben!
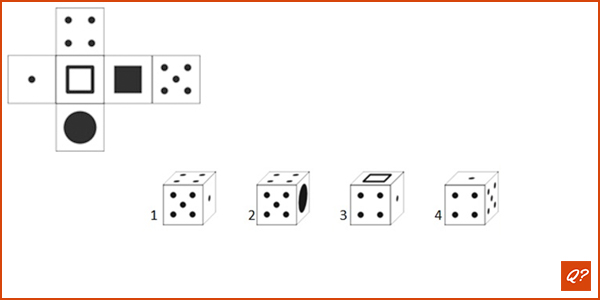
Welk kubus kan NIET gemaakt worden op basis van het uitgevouwen model ?
Antwoord: 2
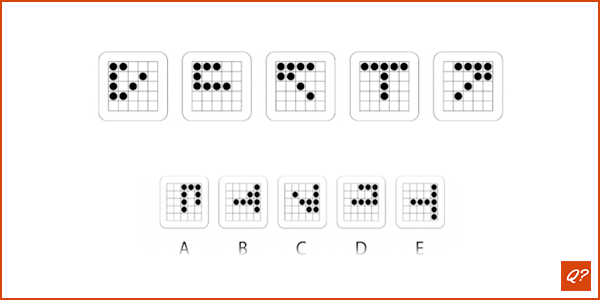
Wat is meest logische vervolg in deze reeks?
Antwoord: D
Twee dobbelstenen worden op een tafel op elkaar geplaatst. Als je rond de dobbelstenen wandelt, wat is dan de som van alle zichtbare ogen?
Antwoord: Als je weet dat tegenovergestelde zijden bij een dobbelsteen steeds de som van 7 geeft, dan weet je ook dat bij de onderste steen 14 ogen zichtbaar zijn en bij de bovenste 15 . Dat geeft dan een totaal van 29 ogen
5 machines doen er 5 minuten over om 5 laptops te maken. Hoeveel minuten doen 100 machines er dan over om 100 laptops te maken?
Antwoord: 5 minuten