Moeilijke raadsels
16 raadsels
Pavlov werd geboren in een kwadratisch jaar (getal dat een kwadraat is) en stierf in het eerstvolgend kwadratisch jaar. Hij werd 87 jaar. In welk jaar werd Pavlov geboren?
Antwoord: 1849
(n+1)² - n² = 87
(n²+2.n.1+1²) - n² = 87
2.n.1 + 1² = 87
2n + 1 = 87
2n = 86
n = 43
43² = 1849
Thomas en zijn vrouw hielden thuis een feestje met 4 andere getrouwde stellen. Elk persoon heeft handen geschud met iedereen die hij of zij nog niet kende. Nadat het handen schudden voorbij was, vroeg Thomas iedereen, inclusief zijn vrouw, hoeveel handen zij geschud hadden. Tot zijn verbazing kreeg Thomas negen verschillende antwoorden.
Hoeveel handen heeft de vrouw van Thomas geschud?
Antwoord: Omdat niemand natuurlijk handen geschud heeft met zichzelf of met zijn of haar partner, heeft niemand met meer dan acht personen handen geschud. En omdat negen personen handen geschud hebben met verschillende aantallen mensen, moeten deze aantallen 0, 1, 2, 3, 4, 5, 6, 7 en 8 zijn.
De persoon die 8 handen heeft geschud, heeft handen geschud met alle andere personen (die dus elk ten minste 1 keer handen hebben geschud), behalve met zijn of haar partner. De partner van de persoon die 8 handen heeft geschud, moet dus de persoon zijn die 0 handen heeft geschud.
De persoon die 7 handen heeft geschud, heeft handen geschud met alle andere personen (die dus elk ten minste 2 keer handen hebben geschud), behalve met zijn of haar partner en de persoon die 0 handen heeft geschud. De partner van de persoon die 7 handen heeft geschud, moet dus de persoon zijn die 1 hand heeft geschud.
De persoon die 6 handen heeft geschud, heeft handen geschud met alle andere personen (die dus elk ten minste 3 keer handen hebben geschud), behalve met zijn of haar partner en de personen die 1 en 0 handen hebben geschud. De partner van de persoon die 6 handen heeft geschud, moet dus de persoon zijn die 2 handen heeft geschud.
De persoon die 5 handen heeft geschud, heeft handen geschud met alle andere personen (die dus elk ten minste 4 keer handen hebben geschud), behalve met zijn of haar partner en de personen die 2, 1 en 0 handen hebben geschud. De partner van de persoon die 5 handen heeft geschud, moet dus de persoon zijn die 3 handen heeft geschud.
De enige overgebleven persoon is degene die 4 handen geschud heeft, en is dus Thomas vrouw. Het antwoord is daarom: Thomas vrouw heeft 4 handen geschud.
Flurkske is een vreemde leugenaar. Zes dagen van de week liegt hij, maar op die ene andere vaste dag spreekt hij altijd de waarheid. De volgende uitspraken deed hij op drie opeenvolgende dagen:
- Dag 1: "Ik lieg op maandag en dinsdag."
- Dag 2: "Vandaag is het donderdag, zaterdag of zondag."
- Dag 3: "Ik lieg op woensdag en vrijdag."
Op welke dag van de week spreekt Flurkske de waarheid?
Antwoord: Flurkske spreekt slechts op 1 dag de waarheid. Wanneer de uitspraak op dag 1 onwaar is, betekent dit dus dat hij de waarheid spreekt op maandag of dinsdag. Wanneer de uitspraak op dag 3 onwaar is, betekent dit dat hij de waarheid spreekt op woensdag of vrijdag. Omdat Flurkske op slechts 1 dag de waarheid spreekt, kunnen deze uitspraken niet beide onwaar zijn. Precies één van deze uitspraken moet dus waar zijn, en de uitspraak op dag 2 moet onwaar zijn.
Stel dat de uitspraak op dag 1 waar is. De uitspraak op dag 3 is dan onwaar, waaruit volgt dat Flurkske de waarheid spreekt op woensdag of vrijdag. Dus dag 1 is een woensdag of een vrijdag. Dag 2 is dan dus een donderdag of een zaterdag. Dit zou echter betekenen dat de uitspraak op dag 2 waar is, wat niet kan. Hieruit volgt dat de uitspraak op dag 1 onwaar is.
Dit betekent dat Flurkske de waarheid sprak op dag 3 en dat dit een maandag of dinsdag is. Dag 2 is dus een zondag of een maandag. Omdat de uitspraak op dag 2 onwaar moet zijn, volgt dat dag 2 een maandag is.
Dag 3 is dus een dinsdag. De dag waarop Flurkske de waarheid spreekt is dus dinsdag.
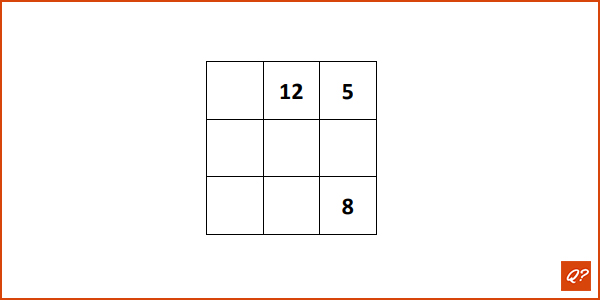
In een magisch vierkant van 3x3 vakjes is de som van de drie getallen in elke rij, in elke kolom en op de twee diagonalen gelijk. Deze som noemt men de magische constante van het magisch vierkant. Wat is de magische constante van nevenstaand magisch vierkant?
Antwoord: 27
Op de kermis kan je meedoen aan het spel “Fruitraden”. Op een tafel staan vier afgesloten dozen. In elke doos zit een verschillend stuk fruit, te weten een appel, een peer, een meloen of een mango. De bedoeling van het spel is natuurlijk om te raden in welke doos welk stuk fruit zit. Er zijn 100 deelnemers die allemaal hun uiterste best doen om alle vier de stukken fruit goed te raden. Na afloop blijkt dat 23 mensen geen enkel stuk fruit goed hebben geraden, 58 mensen precies één stuk fruit goed heeft en 14 mensen precies twee stukken fruit goed hebben geraden. Hoeveel mensen hebben precies drie stukken fruit correct geraden? En hoeveel mensen precies vier?
Antwoord: Exact 3 stukken fruit juist: 0
Exact 4 stukken fruit juist: 5.
Uitleg: Het is niet mogelijk om drie stukken fruit correct te raden: het vierde stuk fruit is dan ook correct! Dus niemand heeft drie stukken fruit correct geraden en 100-58-23-14 = 5 mensen hebben vier stukken fruit correct geraden.
Een figuur bestaat uit drie cirkels en twee lijnen. Hoeveel snijpunten kunnen er maximaal zijn?
Antwoord: Twee cirkels raken elkaar op maximaal twee punten snijden waardoor er zes snijpunten zijn voor de cirkels. De beide rechten hebben ook zes snijpunten met de cirkels en een met elkaar waardoor er maximaal 19 snijpunten zijn.
Denkvraag. In een bak met 12 knikkers zitten er 5 rode, 4 blauwe en 3 gele. Germaine neemt twee knikkers uit deze bak. Wat is de kans dat deze dezelfde kleur hebben?
Antwoord: 19/66
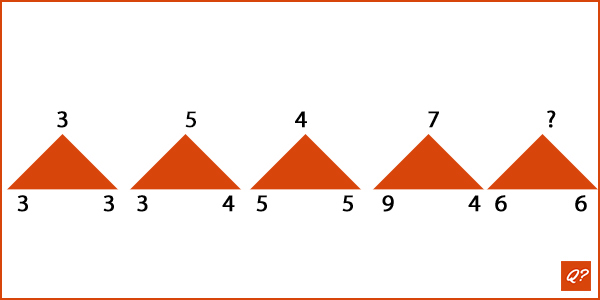
Wat moet er staan op de plaats van het vraagteken?
Antwoord: 6 is het correcte antwoord.
3 + 3 = 6 | zes => 3 letters
3 + 4 = 7 | zeven => 5 letters
5 + 5 = 10 | tien => 4 letters
9 + 4 = 13 | dertien => 7 letters
6 + 6 = 12 | twaalf => 6 letters
Vorm 24 met de getallen 1, 3, 4 en 6 door enkel gebruik te maken van de standaardbewerkingen (+ * / -). Elk getal moet en mag maximum 1 keer gebruikt worden.
Antwoord: 6 / (1 - 3/4)
Marc komt elke dag van zijn werk om 17u met de trein aan. Zijn vrouw zorgt er steeds voor, dat ze stipt op dat moment met de auto bij het station arriveert. Marc stapt dan in en ze rijden huiswaarts. Op zekere dag komt Marc om 16u30 met de trein aan, waarvan zijn vrouw niet op de hoogte is. Hij besluit naar huis te wandelen. Na enige tijd komt hij zijn vrouw tegen, die op weg is naar het station. Marc stapt in en ze rijden naar huis. Nu blijkt dat ze 10 minuten eerder thuis zijn dan gewoonlijk. Hoe lang heeft Marc gelopen?
Antwoord: Zijn vrouw spaart 10 minuten (5minuten heen en 5 minuten weer). Ze ontmoet haar man dus om 16u55. De trein arriveert om 16u30. Marc heeft dus 25 minuten gestapt.